♾️ ‘무한’은 끝이 없다?
– 진짜 그런가요?
“무한하다는 건 끝이 없다는 뜻이다.”
수학 시간에 무심코 들었던 이 말.
하지만 무한에는 단순히 “끝이 없다” 이상의 깊고도 놀라운 비밀이 숨겨져 있습니다.
오늘은 무한이란 무엇인지,
왜 수학자들이 이 개념에 집착했는지,
그리고 우리가 생각하는 “무한”과 실제 수학에서 다루는 “무한”이 어떻게 다른지를
쉽고 흥미롭게 풀어보겠습니다.
1. 무한, 그것은 끝이 없는 세계?
🧠 무한이란 무엇일까?
“무한하다”는 말은 일상에서도 종종 쓰이죠.
- “무한리필”
- “무한한 가능성”
- “무한대의 사랑(?)” 등등…
여기서 말하는 무한은 보통 ‘끝이 없는 것’,
즉, 무한히 계속된다는 뜻입니다.
📏 그런데 수학에서의 ‘무한’은 좀 다릅니다.
수학에서는 무한을 단순히 “엄청나게 큰 수”로 보지 않습니다.
정확하게 측정할 수 없고, 끝도 없으며, 완성될 수도 없는 개념이죠.
예를 들어:
- 자연수 집합 {1, 2, 3, 4, ...}
→ 아무리 세어도 끝이 없습니다 → 무한 집합 - 1 + 1/2 + 1/4 + 1/8 + 1/16 + ...
→ 이건 계속 더해도 끝이 없지만, 결과는 2에 수렴 → 무한급수
이처럼 무한은 ‘무작정 커지는 것’이 아니라,
패턴과 논리를 따라 ‘계속되는 개념’입니다.
2. 무한을 계산한다? – 무한급수와 수렴 이야기

무한한 걸 더하는 게 가능한 일일까요?
👀 놀라운 예시:

계속 더해도 완전히 2를 넘지는 않지만,
점점 2에 가까워진다는 사실!
이런 계산을 무한급수(infinite series)라고 부르며,
결과값이 정해진 값을 향해 가까워지면 이를 수렴(converge)한다고 말해요.
📦 비유로 설명해 볼까요?
상자가 있고, 그 안에 절반만 채웁니다.- 그다음 남은 절반의 절반을 또 채우고…
- 이렇게 계속하면, 상자는 ‘거의’ 꽉 차게 되죠.
이처럼 무한히 반복해도 결과가 어떤 값으로 수렴하면,
수학자들은 그 전체 합을 특정 수로 ‘계산’하는 겁니다.
📘 대표적인 수렴 급수들:
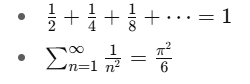
이런 급수의 연구는 수학뿐만 아니라 물리학, 공학, 경제학에서도 중요한 역할을 해요.
3. 무한에도 등급이 있다? – 칸토어의 충격
여기서 끝이 아닙니다.
수학자 게오르크 칸토어는 19세기 말에 무한에는 서로 다른 크기가 있다는 사실을 밝혀냈어요.
"무한한 건 다 똑같이 셀 수 없을 만큼 큰 거 아니야?"
🙅♂️ 아닙니다. 무한도 '크기'가 다릅니다.
예를 들어:
- 자연수 집합: {1, 2, 3, ...} → 가산 무한 (countable infinity)
- 실수 전체: 0과 1 사이의 실수 → 비가산 무한 (uncountable infinity)
🔍 차이는?
- 자연수는 ‘하나씩 셀 수 있는’ 무한
- 실수는 무한히 많은 소수점 자리수 때문에 셀 수조차 없는 무한
→ 실수의 무한이 더 ‘크다’는 뜻이죠.
칸토어는 이걸 수학적으로 증명하며,
“모든 무한은 같지 않다. 무한에도 계급이 존재한다.”
는 혁명적인 통찰을 남겼습니다.
✨ 마무리 – 무한은 개념이지, 실재가 아니다
무한은 현실 속 어딘가에 존재하는 ‘물건’이 아닙니다.
생각 속에서만 존재하는 개념이지만, 실제 세계를 설명하는 데 필수적이죠.
- 우주의 크기
- 시간의 흐름
- 반복되는 계산
- 파이(π) 같은 무리수의 끝없는 소수점
→ 이 모든 데서 무한은 등장합니다.
💬 우리가 ‘무한’을 오해했던 이유
수학적 정의 없이, “무한 = 엄청 큰 수”라고 막연히 생각했기 때문입니다.- 하지만 무한은 ‘점점 가까워짐’, ‘끝없는 반복’, ‘비교 불가능한 크기’라는 논리의 언어예요.