📐 ‘피타고라스 정리’는 왜 그렇게 유명할까?
– 단순한 도형에서 나오는 위대한 수학 공식 이야기
피타고라스 정리는 아마도 대부분의 사람들이 중학교 시절에 처음 접하는 ‘정식 수학 공식’ 중 하나일 거예요.
"직각삼각형에서 빗변의 제곱은 다른 두 변의 제곱의 합과 같다."
즉,

단순한 이 공식이 수학의 전설이 된 이유는 뭘까요?
오늘은 이 정리가 왜 중요한지, 어떻게 쓰이는지,
그리고 얼마나 직관적인 아이디어인지 쉽게 풀어보겠습니다.
1. 이 간단한 공식을 전 세계가 외우는 이유
🔢 공식 자체는 단순하다 정의는 이렇습니다:
- a, b : 직각삼각형의 두 변
- c : 직각삼각형의 빗변
- 공식 :

이 식은 기하학적인 관계를 대수적인 표현으로 풀어내는 대표적인 예예요.
🌍 그런데 이 정리는 '전 세계 공통 언어'
고대 바빌로니아, 인도, 중국 수학에도 유사한 형태가 존재- 유클리드의 《원론》에도 등장
- 오늘날 GPS, 컴퓨터 그래픽, 건축 설계 등에도 사용됨
간단해 보이지만 정말 많은 문제를 이 하나로 해결할 수 있기 때문에 유명한 겁니다.
2. 직각삼각형만의 이야기일까? – 피타고라스의 확장성
처음엔 단순한 삼각형 문제 같지만, 사실 이 정리는 다른 수학 영역으로도 확장됩니다.
📐 2차원 공간 → 거리 공식
두 점 A(x₁, y₁), B(x₂, y₂) 사이 거리:
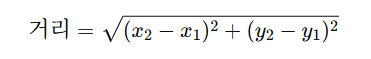
→ 이건 사실상 피타고라스 정리의 변형입니다!
즉, 직각삼각형을 눈에 보이지 않게 만든 것일 뿐이에요.
🧮 3차원 공간에서도?
3차원에서 점 간의 거리:
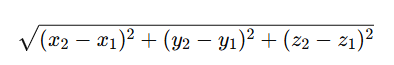
→ 2차원 정리를 또 확장한 형태.
결국, 피타고라스 정리는 공간을 수치로 표현하는 데 핵심적인 역할을 해요.
📈 벡터, 삼각함수, 도형 문제 등에서도 중심축
벡터의 크기 계산- 삼각형 넓이, 원의 반지름 문제
- 고등 수학의 삼각함수 공식 유도
거의 모든 공간/거리 관련 개념이 피타고라스로 귀결됩니다.
3. 머리로도, 눈으로도, 손으로도 느낄 수 있는 정리
피타고라스 정리는 단지 수학자가 증명하는 데 그치지 않고, 직관적으로 이해할 수 있는 드문 공식 중 하나예요.
🧠 머리로 이해하기
a² + b² = c²
→ 두 변으로 정사각형을 만들고, 그 넓이의 합이 빗변의 정사각형 넓이와 같다는 말
예:
- 가로 3, 세로 4인 삼각형
- 빗변은 5가 됨
- 왜냐면 3² + 4² =9+16=25= 5²
👁️ 눈으로 보기 (도형 증명)
피타고라스 정리는 도형적으로도 증명 가능해요.
- 큰 정사각형 속에 작은 삼각형을 배치
- 넓이 비교를 통해 자연스럽게 공식 유도
👉 도형을 그려가며 직접 이해할 수 있는 정리는 피타고라스 정리가 거의 유일합니다.
✋ 손으로 만들기 (직접 실험)
- 종이 자르고 붙여서 피타고라스 정리 확인
- 나무막대나 타일로 만들기
→ 초등학생도 직접 실험으로 증명할 수 있어요!
✅ 요약 – 단순하지만 위대한 공식

💬 마무리 – 수학을 ‘직관적으로’ 배울 수 있다는 것
피타고라스 정리는 수학의 첫 시작점이자,
직관과 논리의 결합이 얼마나 아름다울 수 있는지를 보여주는 예입니다.
수학을 ‘그저 계산하는 과목’이라고 느낄 때,
이 정리를 다시 한번 떠올려보세요.
→ 눈으로 보이고, 손으로 만들 수 있으며, 머리로 이해할 수 있는 수학
그 시작이 바로 피타고라스 정리랍니다.