📘 수포자였던 나도 이해한 개념 – 벡터는 방향 있는 화살표
“벡터가 뭐예요?”를 한 문장으로 설명하면 이렇습니다.
“벡터는 크기와 방향을 함께 가진 화살표 같은 존재예요.”
고등학교 수학에서 처음 접한 "벡터"는 수포자였던 저에게 거의 외계어 같았습니다.
a벡터, b벡터, 단위벡터, 내적, 외적... 갑자기 수학이 물리처럼 느껴지고, 종이에 화살표를 그리고 있는 나를 보며 이런 생각이 들었습니다.
“수학이 왜 갑자기 그림을 그리라고 하는 거지?”
하지만 시간이 지나고 나서 깨달았습니다.
벡터는 일상과 과학, 기술에서 정말 자주 등장하는 '움직임의 언어'였다는 것을요.
오늘은 그런 벡터를 ‘화살표’라는 이미지로 쉽게 풀어보려 합니다.
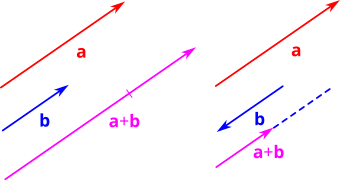
📍 벡터는 방향과 크기를 함께 가진 ‘화살표’
우선, 스칼라라는 개념부터 짚고 갈게요.
- 스칼라는 "크기만 있는 수"입니다. 예: 5kg, 37도, 80km/h
- 반면, 벡터는 크기와 방향이 모두 있는 수예요. 예: 시속 80km로 동쪽 방향 이동
이걸 일상적으로 풀면 이런 차이입니다.

벡터는 이런 식으로 생각할 수 있어요:
🧭 “어느 쪽으로, 얼마나?”라는 질문에 대답하는 수학적 표현
즉, ‘방향성’을 포함한 수치!
이걸 그림으로 표현하면 바로 화살표가 됩니다.
- 시작점: 벡터의 기준 위치
- 화살표 방향: 벡터의 방향
- 길이: 벡터의 크기(또는 세기)
📌 예: 어떤 물체가 오른쪽으로 3m, 또 위쪽으로 4m 움직였다면,
이 두 벡터를 더해서 총 이동 방향(대각선 방향 5m)을 표현할 수 있어요.
(피타고라스 정리 떠오르시죠?)
🚲 벡터는 움직임을 표현하는 언어 – 물리와 일상의 연결
수학 시간엔 괜히 복잡해 보이지만, 벡터는 우리가 사는 세상에 가득합니다.
✅ 현실 속 벡터 예시:
- 자전거를 타고 달릴 때, 우리는 속력뿐만 아니라 어느 방향으로 가는지도 고려합니다.
→ 자전거의 속도는 벡터 - 드론이 하늘을 나는 방향은 X, Y, Z축 모두에 걸쳐 있는 복합 벡터입니다.
→ 드론 제어 = 벡터의 합과 방향 조절 - 게임 캐릭터의 이동 경로도 사실은 좌표 평면 위의 벡터 연산이에요.
→ "앞으로", "대각선", "점프" 모두가 벡터로 계산됨 - 바람은 기상청에서도 방향 + 속도로 보고합니다.
→ "서풍 10m/s" = 방향 있는 벡터 - 내비게이션의 경로 안내도 사실은 벡터 덧셈의 연속입니다.
→ 직진 300m → 우회전 → 직진 500m → 좌회전 = 경로 벡터의 합
이렇듯 벡터는 ‘단순한 수학 문제’가 아니라 세상을 움직이는 수학 언어입니다.
🧠 수학적으로 벡터를 생각하는 법 – 어렵지 않아요
수학에서 벡터는 좌표를 통해 표현됩니다.
예를 들어, 2차원 공간에서의 벡터 a = (3, 4)라고 하면,
- x축 방향으로 3만큼
- y축 방향으로 4만큼
- → 이 벡터의 방향은 대각선, 크기는 √(3² + 4²) = 5
벡터의 핵심 연산은 다음 세 가지입니다:
💡 1. 벡터 덧셈
→ 두 벡터를 이어 붙여서 하나의 총합 벡터로 만드는 것
예: A + B = 한 방향으로 계속 진행한 효과
💡 2. 스칼라 곱 (벡터 × 숫자)
→ 벡터의 크기를 늘리거나 줄이는 것
예: a = (3, 4), 2a = (6, 8) → 같은 방향, 2배로 늘어난 화살표
💡 3. 내적 (dot product)
→ 두 벡터 사이의 각도와 관련
예: 내적이 0이면 두 벡터는 서로 직각 (수직!)
이런 연산들은 처음엔 헷갈리지만,
‘화살표의 방향과 크기를 어떻게 조작하느냐’라고 생각하면 꽤 직관적으로 이해됩니다.
그리고 이 벡터 개념은 점차 공학, 그래픽, AI, 머신러닝, 물리 등 모든 분야에 연결되죠.
✍️ 마무리하며 – 벡터는 '방향 있는 사고'를 만들어주는 도구
처음에는 숫자만 보다가, 어느 순간부터 벡터가 나오고,
방향, 크기, 내적, 외적 같은 말이 나와서 어렵게 느껴질 수 있어요.
하지만 이렇게 생각해보세요:
“세상의 모든 움직임을 수학으로 표현하는 언어”
그게 바로 벡터입니다.
그저 숫자를 넘어서 움직임과 방향을 함께 다루는 방식.
이해하고 나면 정말 강력하고, 직관적이고, 멋진 도구가 됩니다.
화살표 하나로 움직임을 표현하는 세상,
이제 여러분도 ‘벡터’를 보면 더 이상 당황하지 않을 거예요 😊