🔢 ‘정수와 유리수’는 숫자의 층위 – 정리정돈의 시작
"수학이 어려운 건, 숫자가 너무 많기 때문이야…"
그렇다면, 숫자를 정리해보면 쉬워지지 않을까요?
우리는 숫자를 볼 때 종종 '다 똑같은 숫자'라고 생각합니다.
하지만 수학에서는 숫자도 종류별로 나뉘고, 그 층위를 잘 정리하면 복잡했던 개념이 눈앞에 깔끔하게 정리됩니다.
오늘은 ‘정수’와 ‘유리수’, 그리고 그 위에 얹히는 숫자들의 관계를 정리정돈의 관점에서 한번 풀어보겠습니다.

📁 숫자도 분류가 필요하다 – 자연수부터 유리수까지
🔹 자연수 – 수의 시작은 1부터!
우리가 처음 배우는 숫자는 보통 다음과 같죠.
1, 2, 3, 4, 5, …
이 숫자들을 자연수라고 부릅니다.
“사과가 한 개, 두 개…” 이렇게 세는 수를 자연수라고 해요.
🔹 0은 언제 등장했을까?
0은 생각보다 늦게 등장한 숫자입니다.
'없는 것'을 수로 표현한다는 게 철학적이기도 하죠.
수학에서는 0을 포함한 자연수를 자연수 + 0 = whole number (영어식 개념) 이라고도 부르지만,
우리는 0을 따로 인식하기도 합니다.
🔹 음수가 등장하면서 확장된 정수
자연수와 0만으로는 세상 모든 상황을 표현할 수 없습니다.
예:
- “통장 잔고가 -3만원입니다.”
- “온도가 영하 2도입니다.”
이런 '0보다 작은 수'가 음수, 그리고 이 음수까지 포함한 수를 정수라고 합니다.
정수 = { ..., -3, -2, -1, 0, 1, 2, 3, ... }
양수, 음수, 0 모두 포함되죠.
🔹 분수와 소수 – 쪼갠 수는 어디에?
정수만으로는 1보다 작은 양을 표현하기 어렵습니다.
그래서 등장한 게 분수와 소수입니다.
예:
- 피자 반 조각 → 1/2
- 0.25L 음료 → 1/4
이렇게 ‘정수끼리 나눈 수’를 유리수라고 해요.
유리수 = 두 정수 a, b에 대해 a/b (단, b ≠ 0) 형태로 표현 가능한 수
🧱 숫자의 층 구조 – 집처럼 쌓인 수 체계
숫자들은 그냥 흩어진 게 아니라, 계층 구조를 가집니다.
아래처럼 생각하면 훨씬 이해하기 쉬워요.
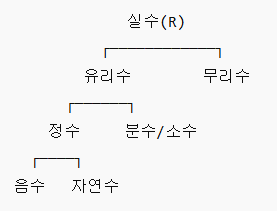
🔹 숫자들의 관계는 확장이다
- 자연수 ⊂ 정수 ⊂ 유리수 ⊂ 실수
→ 마치 상자를 차곡차곡 포개는 느낌이에요. - 유리수는 분수나 소수로 표현 가능
- 정수는 유리수의 일부
- 자연수는 정수의 일부
숫자들의 관계는 “더 넓은 개념 안에 포함되는 구조”입니다.
이것만 이해해도 수학의 많은 개념이 명확해져요.
🔹 유리수는 왜 ‘유리’할까?
‘유리수’(rational number)는 영어로 ratio = 비율에서 온 말이에요.
즉, 정수끼리의 비율로 표현 가능하다는 뜻.
- 1/2
- 5/3
- -7
- 0.75 (왜냐하면 3/4로 표현 가능)
이런 수들은 모두 유리수입니다.
표현 가능한 분수 or 순환소수는 유리수로 분류돼요.
🧩 실생활에서 만나는 정수와 유리수
🔹 통장 잔고, 온도, 계좌 이체
- “통장 잔고 -25,000원” → 음수 (정수)
- “보낸 금액 12,500원” → 유리수 (소수/분수)
금융에서 자주 나오는 '빚'이나 '지급' 개념은 모두 정수/유리수 개념을 포함하고 있어요.
🔹 레시피 비율도 유리수
- 설탕 1.5컵 → 3/2
- 물 0.25L → 1/4
- 비율 2:1 → 정수 비율
요리할 때도 우리는 유리수 세계에 살고 있습니다.
🔹 게임에서의 체력, 경험치, 점수
- 캐릭터 HP: -20 → 죽었음
- 경험치 바: 45.7% → 유리수
- 스코어: 정수
게임 수치들은 대개 정수와 유리수 범위 안에 있습니다.
🔹 정수/유리수 개념 없이는…
- 돈 계산이 불가능
- 온도/시간 단위 사용 불가
- 레시피 오류
- 데이터 분석도 안됨!
숫자의 구분은 계산 그 자체보다, 우리가 ‘세상을 이해하는 방식’에 가깝습니다.
✅ 마무리 – 숫자도 정리가 필요하다
‘정수’와 ‘유리수’를 이해하는 건 단지 시험을 잘 보기 위한 게 아닙니다.
- 숫자들의 구조를 정리하고,
- 어떤 숫자가 어떤 상황에 맞는지 파악하며,
- 세상을 수로 표현하고 예측하기 위한
가장 기초적인 수학의 뼈대입니다.