🧠 논리 명제는 수학의 사고법 – 조건과 결론의 논리 연습
“A이면 B이다” – 조건과 결론은 수학만의 언어가 아니다
“비가 오면 우산을 쓴다.”
“시험에 합격하면 여행을 간다.”
“배터리가 없으면 스마트폰은 꺼진다.”
이 문장들, 모두 수학적인 ‘명제’입니다.
우리가 일상에서 무심코 사용하는 문장들이
사실은 논리와 조건, 결론의 구조를 갖고 있다는 사실,
알고 계셨나요?
수학에서의 명제는 단순히 말장난이 아닌,
복잡한 판단을 해석하고 정리하는 사고의 틀입니다.

명제란 무엇인가? – 조건과 결론의 구조
📌 정의부터 쉽게
명제란 참(True) 또는 거짓(False)을 판단할 수 있는 문장입니다.
예:
- “2는 짝수이다.” → 참
- “3은 5보다 크다.” → 거짓
- “x가 2일 때, x² = 4이다.” → 참
- “오늘 날씨가 좋다.” → 애매함 → ❌ 명제 아님
즉, 판단 기준이 명확해야 명제입니다.
📎 조건 → 결론 : “A이면 B이다”
명제는 조건과 결론으로 이루어진 구조를 가집니다.
- “시험을 보면 합격한다”
→ 조건: 시험을 본다 (A)
→ 결론: 합격한다 (B)
→ 수학적 표현: A ⇒ B
이것은 단순한 문장이 아니라,
AI, 컴퓨터, 법, 철학 등에서도 사용되는 논리의 기초 구조입니다.
🔁 이 명제의 친구들: 역, 이, 대우

원래 명제와 대우는 참·거짓이 같고, 역과 이는 별개의 명제입니다.
이 구조를 이해하면 논리적 사고가 더 정교해집니다.
논리는 사고의 언어다 – 현실 속 명제 찾기
💼 조건부 계약서 속 명제
“프로젝트 완료 시, 보너스를 지급한다.”
- 조건: 프로젝트를 완료했다.
- 결론: 보너스를 지급한다.
이 명제가 거짓이 되려면?
→ 프로젝트를 완료했는데도 보너스를 지급하지 않은 경우
이처럼 조건-결론 구조는
책임, 약속, 보장, 정책 등의 판단에서 핵심적인 역할을 합니다.
🤖 AI 로직은 명제의 집합
인공지능이 “사진 속에 고양이가 있다”고 판단하는 과정은 수많은 명제를 통과해서 나옵니다.
예시:
- “귀가 뾰족하면 고양이일 수 있다” → A
- “수염이 있으면 고양이일 수 있다” → B
- “A와 B 둘 다 참이면 고양이다” → A ∧ B ⇒ C
즉, AI는 끊임없는 조건 판단을 통해 결론을 도출합니다.
이것이 바로 수학적 명제의 세계예요.
🧠 명제 훈련은 사고 정리 훈련
예를 들어:
- “A가 B이면, A가 아닌 경우 B도 아니다.”
→ 대우의 형태입니다. (¬B ⇒ ¬A)
현실 예:
- “학생이면 학교에 다닌다.” (A ⇒ B)
- “학교에 다니지 않는다면 학생이 아니다.” (¬B ⇒ ¬A)
대우가 참이면 원래 명제도 참입니다.
이렇게 논리를 훈련하다 보면 감정과 감각 대신, 명확한 사고로 판단하는 힘이 길러집니다.
수학이 아닌, 모든 분야의 기초 – 명제의 확장성
⚖️ 법과 정책, 규칙도 명제다
법: “음주 상태에서 운전하면 처벌받는다.”
→ 조건(A): 음주 상태에서 운전
→ 결론(B): 처벌
- 운전했지만 술을 안 마셨다면? → A 아님 → 처벌 안 받음
- 술 마셨지만 운전 안 했으면? → A 아님 → 처벌 안 받음
- 술 마시고 운전했는데 처벌 안 받았다면? → 명제가 거짓이 됨
이런 구조는 사회의 공정함과 일관성을 유지하는 데 필수입니다.
🤖 컴퓨터는 명제의 기계
프로그래밍에서의 조건문:
if 조건:
실행문
이것 자체가 바로 명제입니다.
컴퓨터는 오직 True/False만 판단하니까요.
- 조건이 참이면 실행
- 거짓이면 무시
AI, 머신러닝, 게임, 앱 개발 모두 수많은 명제 판단 위에 세워진 구조입니다.
📚 공부와 논술에도 명제가 스며있다
에세이나 논술 문제에서도, “전제 → 주장 → 근거” 구조는 바로 명제적 사고입니다.
- 전제: A
- 근거: A ⇒ B
- 주장: B
이 구조를 정확히 이해하면 논리 오류 없이 설득력 있는 글쓰기가 가능합니다.
🧩 마무리: 명제는 수학을 넘어선 ‘사고의 도구’
📌 핵심 요약
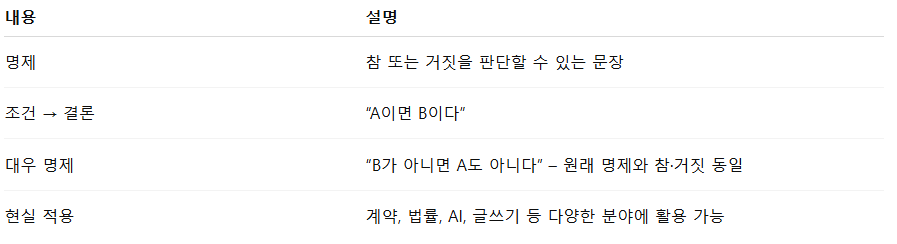
💬 수학은 외우는 게 아니라, 생각하는 방법을 배우는 과정입니다
‘논리 명제’는 수학을 멀게 느낀 사람에게
“아, 수학이 세상을 보는 눈을 길러주는 거구나!”라는
인식을 주는 좋은 개념입니다.