‘로그’는 거듭제곱의 반대말 – ‘몇 번 곱했는가’의 언어
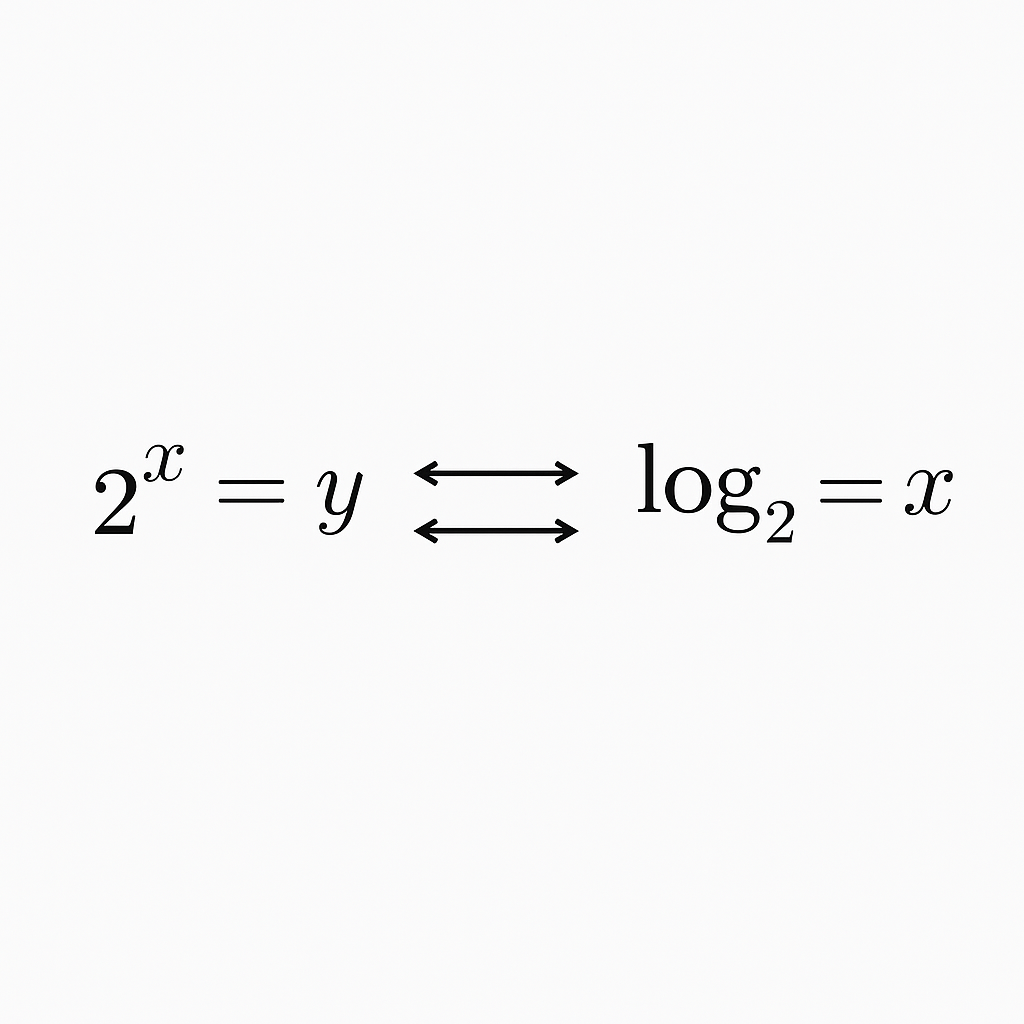
1. 거듭제곱은 익숙한데, 로그는 왜 낯설까?
수포자였던 나에게 "로그(log)"는 딱 수학 포기 지점이었다.
시험 문제는 늘 이랬다.
log₂8 = ?
log₃81 = ?
log₁₀100 = ?
숫자는 보이지만 감은 안 잡히고, 계산도 복잡해 보인다.
그런데 사실 로그는 엄청 단순한 질문이다.
“몇 번 곱해서 이 수가 됐을까?”
이걸 물어보는 게 바로 로그다.
🧠 거듭제곱은 “곱하는 과정”, 로그는 “그 횟수”
예를 들어, 우리가 이미 잘 아는 거듭제곱:
- 2² = 4
- 2³ = 8
- 2⁴ = 16
이건 2를 몇 번 곱했는지를 보여주는 식이죠.
반대로 로그는 결과가 주어졌을 때,
“2를 몇 번 곱하면 이 수가 되는 거지?”
를 묻는 수학입니다.
👉 예시:
- log₂8 = 3 → 2를 세 번 곱하면 8
- log₁₀100 = 2 → 10을 두 번 곱하면 100
그냥 “몇 번 곱했는지”를 묻는 수학적 언어일 뿐이에요.
🧮 로그는 ‘거듭제곱의 거꾸로 보기’
로그는 곱셈의 반대가 아니고,
“거듭제곱의 반대 방향에서 생각하는 수학”입니다.
📌 곱셈의 반대 → 나눗셈
📌 거듭제곱의 반대 → 로그
이 원리를 이해하고 나면, 로그는 훨씬 더 자연스럽게 느껴져요.
단순히 ‘반대’ 개념을 수식으로 옮긴 것이니까요.
2. 로그는 ‘성장의 속도’를 읽는 도구다
로그는 현실에서도 정말 많이 쓰입니다.
특히 폭발적으로 증가하는 현상이나 비율의 크기를 다룰 때 로그는 매우 유용합니다.
📈 예: 바이러스 전파, 로그로 읽다
바이러스 감염은 이렇게 퍼질 수 있어요:
- 하루에 2배씩 증가 → 1명 → 2명 → 4명 → 8명 → 16명 …
만약 감염자 수가 1024명이라고 가정하면,
"도대체 며칠 만에 이렇게 불어난 거지?"라는 질문이 생기죠.
이때 로그를 씁니다:
log₂1024 = 10
→ 하루에 2배씩 늘어난다면, 10일 걸린 것이다.
📌 즉, 로그는 “몇 단계나 증폭됐는가”를 알려주는 도구예요.
🔊 예: 데시벨(dB)도 로그 개념
소리의 세기(데시벨), 지진의 진도(리히터 규모)도 로그 단위를 씁니다.
- 왜?
→ 이들은 작은 변화가 실제로는 매우 큰 차이를 만들기 때문이에요.
예를 들어 데시벨:
- 60dB과 70dB의 차이는 단순히 10이 아니고,
- 실제 소리의 세기는 10배 더 크다는 뜻입니다.
👉 이처럼 “비율의 단계 차이”를 보여주기 위해 로그를 사용하는 거죠.
3. 로그를 감으로 이해하는 비유들
아직도 로그가 어렵게 느껴지신다면,
생활 속에 비슷한 구조를 가진 것들로 바꿔서 생각해보면 금방 이해돼요.
⏳ 로그는 “몇 번 반복했을까?”를 묻는 타임머신
시간을 거슬러 올라가며,
"이 숫자가 이렇게 커지기 전엔 몇 단계가 있었을까?"라고 추적하는 느낌.
- log₂64 = 6
→ 2배, 2배, 2배, … 6번 반복해서 64가 된 것
→ 그러면 반대로 돌아가 보면 64 → 32 → 16 → … → 1
이런 식으로 성장 과정을 추적하는 도구로 로그를 이해해보세요.
📦 로그는 ‘상자를 열어보는 질문’
숫자 1000이 들어있는 상자.
그 상자가 “10을 몇 번 곱해서 만든 거냐”라고 물어본다면?
→ 정답은 log₁₀(1000) = 3
- 첫 번째 10배 → 10
- 두 번째 10배 → 100
- 세 번째 10배 → 1000
즉, 로그는 그 수가 어떻게 만들어졌는지를 “파헤치는 질문”입니다.
🧮 로그와 계산기: 왜 버튼에 따로 있을까?
계산기에도' log '버튼이 따로 있는 이유는,
로그가 단순 계산을 넘어서 패턴의 성장·감소를 분석하는 강력한 도구이기 때문입니다.
지금 이 글을 쓰고 있는 디지털 환경의 속도, 압축률, 보안 알고리즘, 검색 엔진까지…
그 밑바닥에는 모두 로그와 지수 함수가 핵심 역할을 해요.
마무리하며: 로그는 낯설지만, 낯설기만 한 건 아니다
로그는 분명 처음 보면 무섭게 생겼습니다.
log₂16 = 4 같은 식은 공식처럼 보이지만,
결국 “2를 몇 번 곱하면 16이 되는지” 묻는 단순한 질문이에요.
정리하자면:
- 거듭제곱은 “곱하는 과정”,
- 로그는 “그 횟수를 묻는 과정”
- 수식이 아니라 성장과 반복을 추적하는 언어
수포자였던 나도, 이 원리를 깨닫고 나서는
로그 문제가 재밌게 풀리기 시작했어요.
이제 log₃27 = ? 같은 문제가 보이면,
“3 × 3 × 3 = 27 → 정답은 3!”
이렇게 **자신 있게 말할 수 있게 됐습니다. 😊